Πώς να βρείτε την περιοχή ενός ισοσκελούς τριγώνου

Μαθηματικά, και ειδικότερα η γεωμετρία, σύμφωνα με τοοι δημοσκοπήσεις των μαθητών, ένα από τα πιο άγαμα μαθήματα και όλα αυτά επειδή σας κάνουν να μάθετε έναν τεράστιο αριθμό τύπων που στη ζωή το 90% των σημερινών ενηλίκων δεν έχουν βρει πρακτική εφαρμογή. Αλλά, για ένα λεπτό, μαθαίνουμε τύπους, λύνουμε τα προβλήματα, κάνουμε εξισώσεις όχι για το ότι μπορούν να μας βοηθήσουν στη ζωή, αλλά επειδή αναπτύσσει τη σκέψη και τη λογική. Ακόμη και οι αρχαίοι Έλληνες σοφοί είπαν ότι η ανθρώπινη διάνοια μπορεί να μετρηθεί με τη γνώση των μαθηματικών επιστημών. Και δεδομένου ότι αποφασίσατε να εξοικειωθείτε με την εφαρμογή των τύπων για ένα ισοσκελές τρίγωνο - παίρνουμε τον εαυτό μας στο χέρι και διαβάζουμε ολόκληρο το άρθρο.
Πριν αρχίσετε να απαντάτε στην ερώτηση πώς να βρείτετην περιοχή ενός ισοσκελούς τριγώνου και πηγαίνετε στο πρακτικό μέρος του άρθρου, όπου δίνονται οι τύποι και οι υπολογισμοί, ας δηλώσουμε την ίδια την ιδέα για τον εαυτό μας. Ένα ισοσκελές τρίγωνο είναι ένα τρίγωνο στο οποίο δύο από τις τρεις πλευρές είναι ίσες σε μήκος, που ονομάζονται πλευρικές πλευρές. Στην περίπτωση ενός κανονικού τριγώνου, όπου όλες οι πλευρές είναι ίσες, θεωρείται επίσης ισοσκελές, αλλά το αντίστροφο, όταν ένα ισοσκελές τρίγωνο θεωρείται σωστό - είναι ψευδές.
Οι πλευρές του τριγώνου θα πρέπει να ορίζονται, θα το κάνουμε με αυτόν τον τρόπο, όπως φαίνεται στην παρακάτω εικόνα, όπου: a - πλευρές, b-βάση, και h-ύψος.
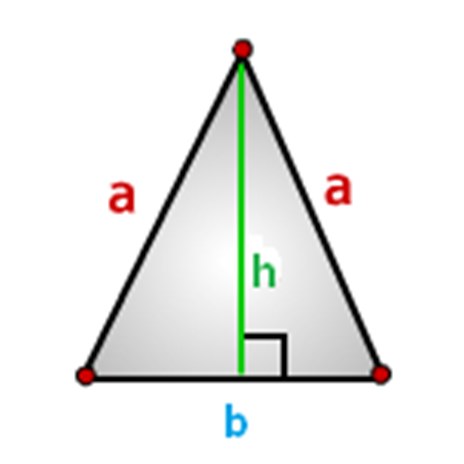
Πώς να υπολογίσετε την περιοχή ενός ισοσκελούς τριγώνου, τύπους.
Αφού έχουμε σημειώσει το ύψος, τις πλευρές και τη γωνία, μπορούμε να ξεκινήσουμε την επίλυση του προβλήματος.
Αρχικά, θα καθορίσουμε τι γνωρίζουμε.
Αν το ύψος και το κάτω - τότε ο κλασικός τύπος (* - το σύμβολο πολλαπλασιασμού):
S = ½ * b * h
Ας αντικαταστήσουμε, για παράδειγμα, τους αριθμούς όπου: h = 16, b = 18, έχουμε τα εξής:
S = 1/2 * 18 * 16 = 9 * 16 = 144;
Η περιοχή ενός ισοσκελούς τριγώνου είναι S = 144 cm2
Υπάρχουν και άλλοι τύποι που θα μας βοηθήσουνστο πώς να γνωρίζουμε την περιοχή ενός ισοσκελούς τριγώνου. Ένας τέτοιος τύπος είναι η μέθοδος του Heron. Ας μην γράψουμε μια σύνθετη φόρμουλα, παίρνουμε, για μια βάση, μια συντομευμένη:
S = ¼ b √4 * a2-b2
Είναι σαφές ότι το b είναι η βάση, και ίσες πλευρές. Ο τύπος είναι κατάλληλος στην περίπτωση όπου το h-height είναι άγνωστο.
Αν αντικαταστήσουμε τις τιμές, α = 6, β = 3, έχουμε τα εξής:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Μπορείτε να υπολογίσετε την περιοχή ίση με τις πλευρές του τριγώνου και τη γωνία μεταξύ των πλευρών:
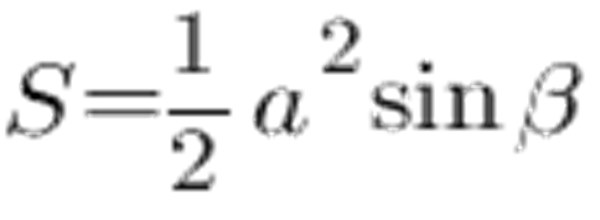
Σύμφωνα με τον ημιτονοειδή πίνακα, η γωνία 45 ° ισούται με 0,7071, η πλευρά a και αφήστε την να είναι 6 cm, έχουμε τα εξής:
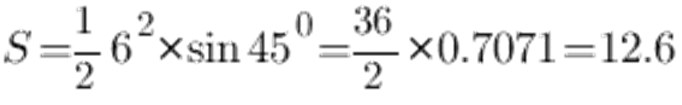
Ως αποτέλεσμα, η περιοχή ισοσκελούς τριγώνου είναι 12,6 cm2.
Υπάρχουν επίσης τρόποι υπολογισμού της περιοχής, συμπεριλαμβανομένων τωνμεταξύ άλλων όσον αφορά ένα ισοσκελές τρίγωνο, αλλά είναι αρκετά περίπλοκη και δεν εφαρμόζονται σε «στοιχειώδη» έννοια των πολύπλοκων υπολογισμών μαθηματικά, του τύπου που δόθηκε παραπάνω. Και μιλάμε για πράγματα που δεν καταλαβαίνουν ακόμα και οι καθηγητές με εμπειρία - δεν αξίζει τον κόπο.
Έτσι, μπορείτε να αναπνεύσετε ένα αναστεναγμό, σε αυτόμια μικρή πορεία γεωμετρίας για την εύρεση της περιοχής ενός ισοσκελούς τριγώνου θεωρείται πλήρης και η γνώση που αποκτάται ως αποτέλεσμα της ανάγνωσης του άρθρου αποκτάται από το "πέντε".














